Optional Lesson: Algorithms Detour - Shortest Path
Overview
In this lesson students will explore the Single Source Shortest Path problem, by solving the problem with pencil and paper first, then by following a famous algorithm that solves the shortest path problem known as Dijkstra’s Algorithm. Even though this is an algorithms detour, there is a strong connection in this lesson to routing algorithms used on the Internet. This lesson also introduces ideas about how we analyze algorithms: looking for correctness, efficiency and running time. As foreshadowing: in the next lesson students will act out another distributed shortest path algorithm used by routers to learn about the Internet dynamically.
Purpose
Algorithms for the Shortest Path Problem have many applications and it’s a widely studied class of problems in computer science. The web abounds with video lectures and presentations about it. Dijkstra’s algorithm, which students follow in the lesson, is one of the most famous shortest path algorithms. While shortest path algorithms are not required knowledge for CS Principles, understanding how algorithms are expressed, and being able to reason about and informally analyze algorithms is. This lesson should set a good foundation for the aspects of expressing and analyzing algorithms that make them challenging and interesting.
Agenda
Getting Started
Wrap-up
Activity
Assessment
Extended Learning
View on Code Studio
Objectives
Students will be able to:
- Reason about a general solution (algorithm) for a problem while examining specific instances of it.
- Informally analyze an algorithm to state how “long” it takes to run relative to the size of the problem.
- Follow a pseudocode algorithm for the single source shortest path problem.
Preparation
- Activity Guide printing:
- Page 1: one copy per student
- Pages 2-9 (8 different graph diagrams): each pair of students needs a copy of one of these pages
Links
Heads Up! Please make a copy of any documents you plan to share with students.
For the Teachers
- Worksheet KEY - Intro to the Shortest Path Problem - Answer Key
- Activity Guide KEY - Dijkstra's Shortest Path Algorithm - Answer Key
- Optional Lessons on Code Studio
For the Students
- Intro to the Shortest Path Problem (optional) - Worksheet
- Dijkstra's Shortest Path Algorithm - Activity Guide
Teaching Guide
Getting Started
Introductory remarks: Say: In the previous lesson you developed an algorithm for the Minimum Spanning Tree (MST) problem. The MST is useful for knowing the most cost-effective way to build or connect a network together. But today we’re going to look at a different problem -- the “Shortest Path Problem” -- which is also a widely studied problem in computer science.
Distribute: Worksheet - Intro to the Shortest Path Problem. (Alternative: teacher demonstration)
Teaching Tips
If you are comfortable explaining the Shortest Path Problem, it might be faster to demonstrate it on a chalkboard using the material covered on the first page of the introductory worksheet. However, you should still have students try their hand at the set of problems on the second page.
- Give individual students time to work on finding the shortest paths for the small examples in the worksheet.
- The worksheet asks students to find the shortest path between two nodes on a series of graphs.
- Then, students will find the shortest path from one node to all other nodes on the graphs.
- Then pair students to compare their answers.
- Did you each come up with the shortest path?
- Was the shortest path always the same?
- Brief share-out.
- Ask for a volunteer idea for an algorithm.
- What makes the algorithm harder/easier than minimum spanning tree?
- Potential responses: easier because you’re told where to start, harder because there is more stuff to keep track of. You need a systematic way to keep track of paths, distances, as you work your way through trying out the nodes.
Wrap-up
Let’s analyze this algorithm.
When we analyze algorithms, there are a few simple questions to ask:
- Is it correct? Will it always solve the problem with a correct solution?
- How much time does it take to run? (Even correct and efficient algorithms take different amounts of time.)
- Will it run in a “reasonable” amount of time; is it efficient?
Is it correct?
- Yes. Beyond intuition, there is a mathematical proof that Dijkstra's algorithm is correct (if all edge weights are positive) and will always find the Shortest Path Spanning Tree for the given source node.
How much time does it take to run?
- Time is an interesting element when talking about computer algorithms. Because there are so many different types of machines with different processing speeds, it’s not really useful to talk about the amount of time an algorithm takes to run in terms of “clock time,” since it will be different on every computer.
- A better indicator is to think about how many “things” the algorithm is making the computer do to run to completion: arithmetic operations, updates to memory, etc. The most important things are those that get performed repeatedly as part of the algorithm. In the shortest path problem, we have to do some processing of every node and every edge. So the shortest path problem is dependent on the total number of nodes and edges in the graph.
- With the minimum spanning tree problem, we created a tree, but it was possible (if not likely) that we didn’t even need to consider every edge in the graph. So with MST, it was dependent on the number of nodes and edges, but we could stop after we found n-1 edges. This is a potential factor when thinking about time.
- NOTE: there are graphs for which the MST has to consider every edge. It has the same theoretical running time in the worst case as SSSP.
- What about the shortest path tree? Is there anyway to stop early? When are you done?
- For Shortest Path you can only stop after you have processed every edge. You cannot stop early. When running the algorithm, it is possible that the very last edge might cause a path to change. Thus, we might say the amount of “time” it takes to run this algorithm is proportional to the amount of time it takes visit every node and every edge once.
- NOTE: Technically, the running time for Dijkstra’s is a little bit more than than just V+E (the number of vertices plus the number of edges). There are computing costs associated with searching for the node that contains the next smallest total distance. For the mathematically inclined: http://en.wikipedia.org/wiki/Dijkstra's_algorithm
- For Shortest Path you can only stop after you have processed every edge. You cannot stop early. When running the algorithm, it is possible that the very last edge might cause a path to change. Thus, we might say the amount of “time” it takes to run this algorithm is proportional to the amount of time it takes visit every node and every edge once.
Is it efficient?
- This algorithm is actually pretty efficient. Discovering the shortest path tree for a node, by looking at every node and edge just once, intuitively feels like you can’t do much better; how could you know the paths without looking at all the edges? Some algorithms on graphs require you to process nodes and edges multiple times. As an easy example to think about: what if we wanted a computer not to find the single source shortest path, but find the ALL the shortest path trees?
Activity
Transition: The reason we have routers is because we want to send messages from our router to lots and lots of different locations. So a more interesting problem on the Internet is finding not just the path from my router to one other router, but the path from my router to EVERY other router!
This is known as the Single Source Shortest Path Problem (SSSP). Today we’re going to look at and analyze a famous algorithm that solves this problem.
Instructions:
Say: You and your partner will be given the algorithm and a graph. And together you will act as the computer, interpreting the instructions and trying to trace out the algorithm and follow its steps.
Part of analyzing an algorithm is trying it out on many different inputs. So, each group will have a different node to start with on the graph and we will test the algorithm to see if it works and then see what we think about it, in terms of its correctness and efficiency.
Activity Guide: Trace Dijkstra's algorithm on a graph.
Distribute: Dijkstra's Shortest Path Algorithm - Activity Guide
- Give each student one copy of the first page (which contains background info, directions, and the algorithm).
- Give each pair of students one graph diagram to use to trace the algorithm’s progress.
- There are different 8 diagrams; each is the same graph but with a different source node indicated.
- Distribute the different diagrams to different pairs of students around the room.
- Students should work in pairs to step through the algorithm and trace it out.
- Typically one student will read the instructions while the other keeps track of information on the graph diagram.
Give students time to work to trace it out.
Share in small groups.
Once students finish, put pairs together (to make groups of 4).
- It’s more interesting if you groups pairs based on which diagrams they were assigned. Here is a suggestion:
- Graph A with Graph E
- Graph B with Graph F
- Graph C with Graph H
- Graph D with Graph G
- Ask groups to discuss the following:
- Compare the shortest path diagrams; these form a tree extending from the source node.
- Are the shortest path trees from two different sources the same?
- What about the path between the two source nodes? (for example: in group A, is their path to E the same as E to A?)
- If so, why? If not, why not?
- Based on your experience, would this algorithm find the shortest path for any graph of nodes and edges?
- Is there a way to stop early? That is, is there a way to stop processing the algorithm because you know you’ve found the shortest path tree? Can you guarantee that you could always stop early? Why or why not?
Assessment
Questions (also in Code Studio):
- Which one of the diagrams below shows the shortest path tree from the source node indicated.
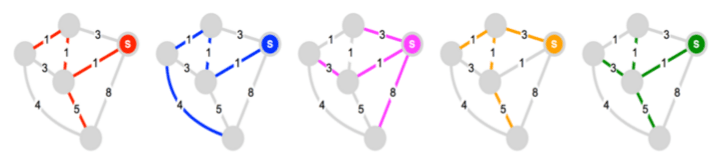
-
Which of the following statements is FALSE about minimum spanning trees (from the previous lesson) and shortest path trees:
a) The minimum spanning tree algorithm you learned does not necessarily need to try every edge.
b) A minimum spanning tree contains the shortest path between the starting vertex and every other reachable vertex in the graph.
c) The shortest path algorithm you learned visits each vertex and edge once.
d) Both the minimum spanning tree algorithm you learned and the shortest path algorithm you learned used a “greedy” approach, choosing the smallest edge first or vertex with the smallest distance value first.
-
Which of the following is NOT something we are concerned with when we write an algorithm?
a) The algorithm is short.
b) The algorithm is correct.
c) The algorithm is efficient.
d) The algorithm is understandable.
-
If a graph has 10 nodes and 33 edges, how many nodes and edges will be visited/processed as a result of running Dijkstra’s algorithm?
-
When analyzing algorithms, why doesn't the amount of real time (clock time) tell us very much about the algorithm's "efficiency"?
Extended Learning
- Dijkstra’s algorithm: http://en.wikipedia.org/wiki/Dijkstra's_algorithm
- Interactive algorithm visualization tool: http://visualgo.net/sssp.html
- A 9-minute lecture on Dijkstra’s algorithm: https://www.youtube.com/watch?v=mv4r7F82doA
- Lesson Overview
- Student Overview
Student Instructions
Student Instructions
Recall when you built your binary message sending device. Why did we decide to send a message as a sequence of states (A and B) rather than modifying our devices to represent more states (State C, State D, State E, ...)?
Student Instructions
Provide an example of a question that could NOT be answered with a single binary message. Explain why this is the case, making reference to the definition of a binary message.
Student Instructions
How did collaboration impact the development of your protocol? What challenges did working in a group present and in what ways did it positively impact your final product?
Standards Alignment
View full course alignment
CSTA K-12 Computer Science Standards (2011)
CT - Computational Thinking
- CT.L3B:3 - Critically examine classical algorithms and implement an original algorithm.
- CT.L3B:4 - Evaluate algorithms by their efficiency, correctness, and clarity.
- CT.L3B:6 - Compare and contrast simple data structures and their uses (e.g., arrays and lists).
Computer Science Principles
4.1 - Algorithms are precise sequences of instructions for processes that can be executed by a computer and are implemented using programming languages.
4.1.2 - Express an algorithm in a language. [P5]
- 4.1.2A - Languages for algorithms include natural language, pseudocode, and visual and textual programming languages.
- 4.1.2B - Natural language and pseudocode describe algorithms so that humans can understand them.
- 4.1.2C - Algorithms described in programming languages can be executed on a computer.
4.2 - Algorithms can solve many but not all computational problems.
4.2.1 - Explain the difference between algorithms that run in a reasonable time and those that do not run in a reasonable time. [P1]
- 4.2.1A - Many problems can be solved in a reasonable time.
- 4.2.1B - Reasonable time means that as the input size grows, the number of steps the algorithm takes is proportional to the square (or cube, fourth power, fifth power, etc.) of the size of the input.
4.2.4 - Evaluate algorithms analytically and empirically for efficiency, correctness, and clarity. [P4]
- 4.2.4A - Determining an algorithm’s efficiency is done by reasoning formally or mathematically about the algorithm.
- 4.2.4B - Empirical analysis of an algorithm is done by implementing the algorithm and running it on different inputs.
- 4.2.4C - The correctness of an algorithm is determined by reasoning formally or mathematically about the algorithm, not by testing an implementation of the algorithm.
- 4.2.4D - Different correct algorithms for the same problem can have different efficiencies.
- 4.2.4G - Efficiency includes both execution time and memory usage.
