Lesson 5: Representing Numbers
Overview
In this lesson, students learn about the binary number system. With a set of cards that represent the place values in a binary (base-2) number system by a collection of dots, students turn bits "on" or "off" by turning cards face up and face down, then observe the numbers that result from these different patterns. Eventually, students extend the pattern to a generic 4-bit system.
Purpose
Students learn how to use the binary system to represent integers. Unlike ASCII, which is presented as an arbitrary mapping of bit patterns to characters, binary numbers are introduced within the context of patterns of numbers. Students use the patterns to determine the binary representations of different numbers, rather than simply looking them up in a table.
This lesson borrows heavily from a similar activity in CS Unplugged.
Assessment Opportunities
-
Use a binary system to represent numbers.
Activity Guide, page 1: Student answers should match the key, noting that the last three questions may have different answers student to student.
-
Extend a representation system based on patterns.
Activity Guide, page 2: On the top of the page, students should correctly extend the pattern to 5- and 6-bit numbers.
Agenda
Lesson Modifications
Warm Up (10 mins)
Activity (40 mins)
Wrap Up (10 min)
Extension (10 mins)
View on Code Studio
Objectives
Students will be able to:
- Use a binary system to represent numbers.
- Extend a representation system based on patterns.
Links
Heads Up! Please make a copy of any documents you plan to share with students.
For the Teachers
- Representing Numbers - Exemplar
For the Students
- Representing Numbers - Activity Guide
- Number Cards - Manipulative
- How Computers Work - Data and Binary - Video (download)
Teaching Guide
Lesson Modifications
 Attention, teachers! If you are teaching virtually or in a socially-distanced classroom, please read the full lesson plan below, then click here to access the modifications.
Attention, teachers! If you are teaching virtually or in a socially-distanced classroom, please read the full lesson plan below, then click here to access the modifications.
Warm Up (10 mins)
Discussion Goal
Goal: In this and the following lessons students will be learning a new system to represent numbers using on-off signals. Motivate this activity by thinking back to the kinds of information students eventually will want to represent with this system. If students need help brainstorming give them a couple examples, e.g. age, their height, their birthday, the number of friends they have, the cost of items, an item's rating, etc.
Prompt: Create a list of all the information you might want to represent to a computer as a number. Here's some ideas to get you started
- An online store (what kinds of numbers does a store keep track of?)
- A social media profile (what things about you or your friends are numbers?)
Discuss: Students should brainstorm independently, then share with a partner, then finally discuss as a whole class.
Remarks
Numbers are a really useful and important way to represent all kinds of information. If we want to represent numbers to a computer, we're going to have to learn a new system that allows us to do that.
Activity (40 mins)
Teaching Tip
For younger students, you may want to stop the activity after they have finshed the first page of the worksheet. This means that they will not need to go online for any of the lesson.
Group: Put students into pairs.
Distribute: Give each pair a copy of the activity guide and a set of number cards.
Binary Cards
Teaching Tip
This activity models a base-2 number system for the student. However, it is not necessary for the students to understand the math behind the patterns that they are creating. Students should focus on the fact that they are using a binary system (face up/face down) to represent information.
Model: Go through the example problem as a class. Ask students to arrange cards face up and face down so that exactly thirteen dots are showing. (It is important that each group uses only one set of cards.) After some trial and error, students should see that the 8, 4, and 1 cards should be face up, and the 2 card should be face down. (U U D U)
Allow students to complete the rest of the page in pairs.
When all students have finished the page, ask them to come back together as a class and share their answers.
Student answers may vary for some questions. You can use the following guide to check their work.
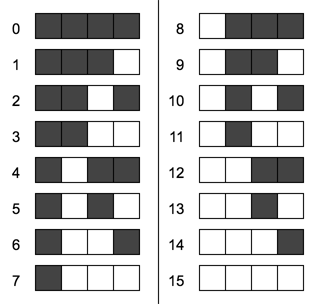
Discussion Goal
Goal After some discussion, students should note that there is only one way to represent any particular number in this system. This is an important point to bring out because it would be confusing if two patterns meant the same thing.
Prompt: Was there more than one possible answer for any of the problems?
Allow students to check with other pairs and try to find another way to represent the numbers.
Using the Pattern
Send students to the online lesson.
Allow students to complete the second half of the worksheet, with the support of the widget, as seen below.
Discussion Goal
Goal Students should recognize that the patterns of the numbers and the rules that they followed to get them allowed them to figure out how a number would be represented, without using a table, as they did in ASCII.
Prompt: When we learned ASCII, you had to use a table to look up each letter. For binary numbers, you were able to represent your numbers without a table. How did you do that?
Allow students to discuss their ideas in pairs before bringing them back to the group.
Remarks
With these cards, we've created a binary system to represent numbers. Because we used a pattern that we can follow as our numbers get bigger, our system can work for as high as we can count. Of course, our cards will eventually run out of space to put the dots, so we're going look at a tool that will help us to use binary numbers in the hundreds.
Wrap Up (10 min)
Discussion Goal
This wrap up gives students a chance to reflect on binary representation systems in general, as well as the specifics of binary number representation. Ensure that students understand that all binary number systems use two elements, that they must be unambiguous, and that everyone who uses the system must have a common understanding of the rules.
For the second question, there are many possible acceptable answers. However, ensure that the idea that the patterns used for binary numbers are not arbitrary comes up in the discussion.
The last question is more open ended to give teachers insight into what might be top of mind challenges for students in understanding binary representation.
Journal 3-2-1
Prompt: So far, we've looked at how we could represent text, images, and numbers in binary.
3. What are three ways that the binary representation systems are all the same?
2. What are two things that are special about the way we represent numbers in binary?
1. What is one challenge in representing information on a computer?
Extension (10 mins)
Prompt: So far, we've looked at how we could represent text, images, and numbers in binary. Are there any other types of data that you use on your computer that need to be represented?
All students to call out different types of data, such as music, videos, etc.
Remarks
Those are all types of data that need to be represented in binary. We're going to watch a video that explains a little bit more about how this works.
Display: Play the "Binary and Data" video.
- Lesson Overview
- Teacher Overview
- Student Overview
- Representing Numbers - Exemplar (PDF | DOCX)
Teaching Tip
Answers for this level can be found in the exemplar linked on Level 1.
Student Instructions
5-Bit Number
When you only had four bits, the highest number that you could make was fifteen. Now you'll have a chance to work with more bits to make higher numbers.
In this activity, the dots are replaced with numbers, but you still add up everything that's showing to see what number the binary code stands for. The left-most bit doesn't have a number yet, so you'll have to give it one.
Do This
- Click on the bits to turn them on and off, and see the different numbers you can make.
- With your partner, discuss the pattern in the numbers. Decide what number you think should go in the left most box.
- Click "Edit" to change the value of the left most bit.
- Once you've decided on the value, try to make the following numbers: 16, 27, 31
Teaching Tip
Answers for this level can be found in the exemplar linked on Level 1.
Student Instructions
6-Bit Number
This widget helps you to calculate 6-bit binary numbers.
Do This
- With your partner, answer the following questions:
- What's the biggest number you can make with this widget?
- The record for most skips by a dog and person in one minute is 59. How would you encode 59 in binary?
Teaching Tip
Answers for this level can be found in the exemplar linked on Level 1.
Student Instructions
Decoding multiple numbers
Here's a widget that can calculate numbers of 4, 5, or 6 bits. You can use it to find the two world records encoded in the binary string below.

- Most number of people lifted and thrown in two minutes. (4 bits)
- Most canned drinks opened by a parrot in one minute. (6 bits)
Do This
- Decode the two numbers from the binary string.
Teaching Tip
Answers for this level can be found in the exemplar linked on Level 1.
Student Instructions
Decoding multiple numbers
Here's a widget that can calculate numbers up to to eight bits. You can use it to find the values of the two world records below.
Don't forget to make sure that the "1" bit is always the right most bit. If you have extra bits on the left side of the widget, just keep them turned off.

- Longest tail on a dog (in inches) (5 bits)
- Most spoons balanced on someone's face (5 bits)
Do This
- Decode the two numbers from a the binary string.
- Hint: You'll need to read the numbers in order, with the first answer using the first five bits, and the second answer using the five bits after that.
Teaching Tip
Without knowing the length of each of the numbers, students will not be certain of their answers, but they should be able to at least find one possible solution. Allow students to discuss any differences in their answers. They should eventually see that they need to know the bit length of each number to answer the question.
Student Instructions
Decoding multiple numbers
Here's a new bit string. This time, you don't know the bit length of the two numbers. Try to decode the numbers without knowing the bit length.

- Largest wind chime, in feet (? bits)
- Furthest arrow shot with someone's feet (in feet) (? bits)
Do This
- Try to decode the two numbers from the binary string.
- Discuss with your partner why you cannot know for sure whether your answer is correct.
Teaching Tip
Answers for this level can be found in the exemplar linked on Level 1.
Student Instructions
Bit Length
If you don't know how many bits long each number is, you won't be able to decode a string of numbers.
For example, the following binary string could be decoded many different ways.

If you split the string like this, the string reads 10, 84.


If you split it like this, the string reads 42, 20.


To solve this problem, people agree on a fixed length for every number. The following string uses the same two numbers, but each number takes up exactly eight bits, no matter how many bits it actually needs.

Do This
- Use the binary widget to decode the string that uses eight bit numbers.
- Check you answer with a partner to see whether you got the same answer.
- Binary and Data
- Teacher Overview
- Student Overview
Discussion Goals
Th goal of this discussion is to have the students think more deeply about the purpose of binary. For the first question, they may want to return to their ASCII character sheets and see how the computer would interpret the same binary sequence as a number. For their image representation, they may wonder whether it is even useful to interpret the binary sequences as numbers. In the end, the purpose of defining all data as numbers is less about the "reality" of what the ones and zeros represent, and more about how binary is traditionally interpreted.
For the second question, allow students to think of different ways that the computer would distinguish between different types of data. While it's not necessary for students to come up with any specific answer, challenge them on any ways that involve human interpretation of context, such as knowing that a name is most likely text and an age is most likely a number. Assure them that they will look at the problem again in a couple of lessons.
Questions to Consider
- Why are all the types of data on the computer stored as numbers?
- If everything is stored as a number, how do you think the computer tell the difference between numbers, letters, images, and sound?
Standards Alignment
View full course alignment
CSTA K-12 Computer Science Standards (2017)
DA - Data & Analysis
- 2-DA-07 - Represent data using multiple encoding schemes.
