Unit4
Ch. 1
1
2
3
4
5
6
7
8
9
10

Lesson 9: Public Key Cryptography

Widget

Overview

This is a big multi-part lesson that introduces the concept of public key cryptography which is an answer to the crucial question: How can two people send encrypted messages back and forth over insecure channels (the Internet) without meeting ahead of time to agree on a secret key? In a nutshell, there are two main principles we want students to understand:

  1. The mechanics of communication with public key cryptography
  2. The basic mathematical principles that make it possible

The lesson gets at these two core ideas through a deliberate chain of thought experiments, demonstrations, activities and widgets. All parts are building blocks that lead to deeper understanding of how it works.

Purpose

This is a fairly hefty lesson because the underlying ideas are subtly quite sophisticated. It's worth noting that much of the material here - all but the highest level takeaways - are beyond the scope of what's covered on the AP exam. Students need to know the basic public key encryption process, and what asymmetric encryption is. For programming they need to know how the modulo operation works.

Our purpose here is to reveal some of the magic that happens every day on the Internet to enable secure transactions. To many the fact that encrypted messages can be sent between parties who have never met before is both taken for granted and opaque. Our belief is that understanding how it works with some depth - getting to experiment with the mathematical principles that make asymmetric keys possible, and the resulting encryption hard to crack - is deeply satisfying.

The widget in the lesson mimics the RSA encryption algorithm (with smaller numbers and slightly easier mathematics).

Agenda

Getting Started (5 mins)

Activity 1 (15 mins)

Activity 2 (30-45 mins)

Activity 3 (30-45 mins)

Wrap-up (10 mins)

Assessment

Extended Learning

View on Code Studio

Objectives

Students will be able to:

  • Explain what the modulo operation does and how it operates as a "one-way" function
  • Follow an asymmetric encryption algorithm to encrypt a numerical message using the Public Key Crypto widget.
  • Explain the difference between symmetric and asymmetric encryption.
  • Describe the basic process of encrypting data using public key encryption
  • Explain the benefits of public key cryptography

Preparation

This lesson will likely take two days to complete. Preparing for these activities the first time will take some time. Once you've been through it once, the activities actually go quicker than you might expect.

Suggested Prep for Day 1 (Steps 1-3)

  • Prepare the Cups and Beans demonstration (you need cups and beans)
  • Understand the modulo thought experiment with pictures of clocks
  • (Optional) Paper copies of "multiplication + modulo" activity guide

Suggested Prep for Day 2 (Step 4 + wrap up)

  • Practice using the "modulo clock"
  • Practice and Prepare for the using and demonstrating the public key crypto widget

Links

Heads Up! Please make a copy of any documents you plan to share with students.

For the Teacher

For the Students

Vocabulary

  • asymmetric encryption - used in public key encryption, it is scheme in which the key to encrypt data is different from the key to decrypt.
  • modulo - a mathematical operation that returns the remainder after integer division. Example: 7 MOD 4 = 3
  • Private Key - In an asymmetric encryption scheme the decryption key is kept private and never shared, so only the intended recipient has the ability to decrypt a message that has been encrypted with a public key.
  • Public Key Encryption - Used prevalently on the web, it allows for secure messages to be sent between parties without having to agree on, or share, a secret key. It uses an asymmetric encryption scheme in which the encryption key is made public, but the decryption key is kept private.
  • symmetric encryption - an encryption scheme in which the key used to encrypt data is also used to decrypt (contrast with: asymmetric encryption)

Support

Lesson Forum

Report a Bug

Differentiation and accommodations for this lesson

Teaching Guide

Getting Started (5 mins)

How do you get the encryption key?

Prompt: "How can two people send encrypted messages to each other if they can't communicate, or agree on an encryption key ahead of time, and the only way they have to communicate is over the Internet?"

  • You should assume that an adversary is always secretly eavesdropping on their conversation too.
  • With a partner come up with a strategy they could use to send encrypted messages.

Discussion Goal

Goal: Realize the difficulty of the problem. No form of symmetric encryption will work. There is no way for parties to establish a shared key without agreeing ahead of time in a way that secures it from an observer. Hopefully some students will recall from the video in the last lesson the ideas of using different keys - one to encrypt data and one to decrypt it.

Possible Responses: Students may come up with some fantastic ideas, but most will amount to some secret ahead-of-time agreement about a key, or simply some strategy that obscures the key ("security by obscurity").

Discuss

  • Give students a few minutes to discuss
  • Don't let the discussion go too long
  • Direct the conversation toward the idea from the video of using different keys - one to encrypt and one to decrypt.

Recall asymmetric keys were mentioned in the cryptography video.

Transitional Remarks

Today we're going to dig in a little bit deeper to how this idea of using different keys actually works. The ideas behind how it works are sophisticated, and so to get a deeper understanding we're going to do a series of short activities that stringing together several different ideas, bringing them all together in the end.

Ready? Here we go!

Activity 1 (15 mins)

Step 1: A New Analogy - Cups and Beans

Teaching Tip

Remind students - we're still a ways from the real thing but we're taking baby steps to string ideas together.

Groups:

  • Option 1 (preferred): Teacher Demo. We recommend doing this activity as a teacher demonstration in the interest of time. Instructions and teacher guide below

  • Option 2: Groups of 3 Students. You can have students work through an activity guide that explains it as well. It will take more time. (Optional) Public Key Bean Counting - Activity Guide

Materials: Cups and Beans - enough for a demonstration (or for groups of 3, if running as student activity)

Display: You may want to display a picture of a jar full of candies to give a visual for the analogy you're about to explain.

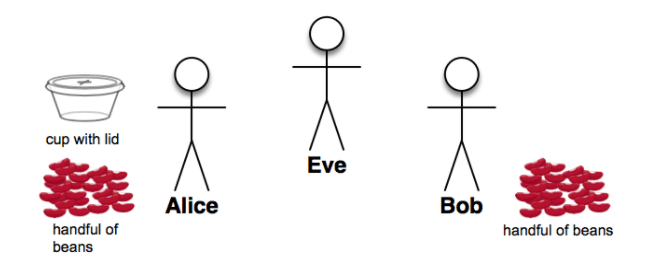
Teacher Demonstration - Cups and Beans

The lock box analogy from the video is a good start, but our first step to seeing how public key cryptography works requires us to look at the same process of using public and private keys but with an analogy that goes a step further.

Full Teacher Guide: Public Key Bean Counting (Cups & Beans Activity) - Teacher Demonstration Guide

Discussion Goal

The cups and beans demo showed basically the same public/private key analogy as the lockbox in the video.

Similarities:

  • For Bob to send a message to Alice he needs to obtain a public key, which we can use to "lock" a message
  • Only Alice can "unlock" the message
  • Bob and Alice do not need to agree on a key ahead of time
  • Alice never lets her private key out in public

Differences:

  • Beans in cups is closer to how data is encrypted - beans are data, sealed in the jar is encrypted
  • Eve (or anyone else) could only guess what was in the jar even though it passed right in front of/through them over the "Internet"
  • At no point was the secret message ever out in public, or sent unsecured.
  • Closer to reality: Notice how the public key itself is a form of encrypted message. But it's used to encrypt something else

Setup and Activity Summary:

  • Alice choose a private key (some number of beans)
  • Alice make a "public key cup" by placing beans in a clear cup and sealing it
  • Pass the cup to Bob over the "Internet"
  • Bob grab the "public key cup" and add a secret number (of beans) to it
  • Pass the cup back to Alice over the "Internet"
  • Alice open cup and subtract the number of beans she added originally
  • What's left is Bob's secret number

Discuss: Relate this process using cups and beans to the lockbox analogy from the video. What's similar? What's different? What took place of the public key? The message? The private key?

  • Let students discuss for a minute
  • You may review the "what's the point" items and table at the end of teacher demonstration guide
  • Ensure that students see how the cups and beans process was similar to the lockbox process.

Remarks

Okay so that's one step. We now have a clearer idea of the public key encryption process. If we can keep extending this we'll have a solution to the problem of how two people can encrypt messages without meeting ahead of time.

Next we need to see how actual data is encrypted rather than beans in cups.

To learn that, we'll need to string a few more ideas together.

Activity 2 (30-45 mins)

Step 2: Modulo - The operation behind public key encryption

The next idea we need to add is an important mathematical operation called "modulo".

Remarks

The cups and beans demonstration showed us how the mechanics of public key cryptography works.

It’s a big deal that asymmetric encryption allows for two parties to send secret messages to each other over public channels without having to agree on a secret encryption key ahead of time.

Now let’s look at the mathematical principles that allow private and public keys to work.

"Clock Arithmetic Thought Experiment"

What's Modulo?

The modulo operation is a math operation that returns the remainder from dividing two numbers. For example, in classic division 13/5 is 2 Remainder 3 . The mod operation gives the remainder portion. So we would say 13 MOD 5 = 3.

There is a well known visual analogy for modular arithmetic using clocks since modulo is often thought to "wrap" the number system. If, for example, you use 12 as a modulus then any result must be in the range 0-11 since those are the only possible remainders. Similarly, no matter how many hours you count off on a traditional analog clock, there is a limited number of hours (1-12) that the hour hand can be pointing to. It's even called "Clock Arithmetic" in some places wikipedia: modular arithmetic

The modulo operation is important for cryptography because it can act as a one-way function - the output obscures the input.

No need to linger

The purpose of this thought experiement is to understand the clock analogy for modulo. It is a setup for the next step.

Students should understand the concept of numbers that "wrap" around the clock and that the "size" of the clock could be arbitrary - it doesn't have to be 12. The same principle would apply for a "clock" of any size.

Teacher Guide: Use the Modulo Clock Thought Experiment - Teacher Guide

Here is a summary:

Materials: two pictures of analog clocks - one with hour hand at 4:00 and another at 3:00.

Display: picture of clock at 4:00. You can use this interactive clock rather than pictures if you like.

Run the thought experiment: Use Full Teacher Guide for details: Modulo Clock Thought Experiment - Teacher Guide

Key Points of the thought experiment:

  • This "clock" operation is called Modulo
  • Modulo is an actual math operation - it's the remainder after division
  • The clock is a useful visual to think about, but the size of the clock is arbitrary
  • the same principle of "wrapping" around the clock would apply no matter how many ticks were on the clock.

Step 3: The Mod Clock Widget and Multiplication + Modulo

Mod Clock + Multiplication Goals

This step has two goals:

  1. Allow students to play with the "Mod Clock" widget to get a sense for how modulo works
  2. See how multiplication combined with modulo can lead to "computationally hard" problems to solve

In particular we want students get a feel for how and why guessing the blank value is pretty hard in: A * ____ MOD M = R even when you know A, M, and R.

For example, guess the missing value in this: 47 * ____ MOD 51 = 1 you are essentially reduced to random guessing.

Remarks

Modulo is important for cryptography as a one way function - you can't tell based on the remainder what went into the clock.

To understand how it's used in cryptography, we're going to investigate what happens when we use simple multiplication to produce the number we input into the clock. There are certain properties that are useful when we combine simple multiplication with modulo.

Multiplication + Modulo Activity

Group: Have students partner up in groups of 2 or 3

Distribute: Activity guide Multiplication + Modulo - Activity Guide

Code Studio: Direct students to the "Mod Clock Widget" in code studio.

  • Demonstrate a few quick sample inputs to show how the clock size can change and numbers "wrap around"
  • The big number in the middle is the remainder, the result of the modulo operation

This is not on the AP exam

Students do not need to memorize or be facile with these mathematics for the AP Exam.

The modulo operation is part of the AP pseudocode and there might be simple programming questions on the exam that use it.

However, the mathematics for Public Key Cryptography is beyond the scope of the course. We are giving it a small treatment here to expose a statement from the AP CSP framework: 6.3.1I Cryptography has a mathematical foundation.*

Content Corner

You cannot solve it like a typical equation in math class because there are many equations. If you are looking for A * ___ MOD 13 = 1 for example, what you are really trying to find is a number that you could multiply by A that comes out to one of a list of infinite values: 1, 14, 27, 40, 53,...and so on.

Student do the activity: students should work with a partner to work through the problems on the activity guide.

Circulate as students work. Make sure that they are trying out the problems given which ask them to try to guess numbers. They should also be using the Mod Clock to check their results.

Students should get a feel for this general formula: (A * B) MOD M and its properties, because it is the foundation on which we'll create public and private keys in the next step.

Discuss: "Why is it hard to guess which numbers multiplied together produce the result?"

These points are made at the bottom of the activity guide. After students have worked on the problems for a bit they should be able to give a few responses here such as:

  • You cannot solve it like an equation in math class
  • Numbers kind of jump all over the place
  • You kind of have to just guess randomly, or at least systematically try every number.

Activity 3 (30-45 mins)

Step 4: Use the Public Key Crypto Widget Activity

Activity Goals

  • Use the widget to practice the public key encryption process
  • Explain how asymmetric encryption works at a high level
  • See how multiplication + modulo can be used to create asymmetric keys
  • Try to crack messages encrypted with multiplication+modulo

The public key crypto widget showing Alice's screen

Bringing it home

Okay, now to finally bring everything together. This is last and final step in which we'll see how we can use the math we just learned about to create public and private keys.

Real Public Key Cryptography?

It might be hard to believe but this widget is pretty close to mimicking real RSA encryption.

When you use RSA "for real" you have to generate a public/private key pair using software on your computer. You put the public key somewhere that someone can grab, like your personal web page (there are other ways too.)

You keep the private key on your computer and never distribute it.

Most of the time your computer handles the encryption and decryption behind the scenes.

If you would like to try or demonstrate for your students, you can. Just google "RSA Keygen" and follow instructions for your type of computer.

The Public Key Crypto Widget Activity

Teacher Guide: Use the Public Key Crypto Widget Activity - Teacher Guide which contains details for each step of this process.

Group: Put students into groups of 2 (to play just Alice and Bob initially).

  • Each student should be at their own computer, but within speaking distance

Display: the Public Key Crypto Widget Instructions page (in code studio)

  • You can ask students to go to that page as well if you want them to read it now, or just have it displayed for you to review the instructions.

Summary: Use the teacher guide, but here is a summary for reference:

Answers to some FAQs about the widget

Clock size is chosen randomly by Alice but there is a set list of values to choose from. The clock sizes in the list provided are prime numbers between 1 and 10,000. This ensures certain properties of the encryption.

Alice’s private key is also chosen at “random” but there is also a list to choose from. We’ve computed pairs of public/private keys behind the scenes so they have the necessary mathematical relationship. Alice simply has to pick one.

Bob is sending a secret number to Alice, not vice-versa. In public key cryptography for Bob to send a secret to Alice, alice has to act first, producing a public key for Bob to use.

Bob can send any number to Alice - as long as the number is between 0 and (clockSize - 1.)

The clock size limits the range of values - the secret numbers that Bob and Alice use are confined to the output range of the mod clock. For example: if the clock size is 13, then Bob can only send a secret number in the range 0-12. If the clock size is 253 then the secret values can be 0-252.

Part 1: Introduce the widget (10 mins)

  • Introduce the Public Key Crypto widget providing the background and instructions given on the Instructions page in code studio. Make sure to point out the similarities and differences between using this widget and cups and beans.

  • Demonstrate the first step of using the widget. (Click past the the instructions page to get to the widget if necessary)

Part 2: Just play Alice and Bob (5 mins)

  • With a partner, just play Alice and Bob and exchange a few numbers to get the hang of it. Communicate by just speaking out loud. Exchange roles at least once. Verify that you can encrypt and decrypt messages.

Part 3: Show how Eve works (10 mins)

  • After pairs have gotten the hang of playing Bob and Alice, regroup to review how Eve works. Display Eve's screen in the widget.

  • Pick 2 students on opposite sides of the room to play Alice and Bob and demonstrate intercepting their spoken broadcasts and entering the info in Eve's screen.

Part 4: Experiment with cracking bigger numbers (5-10 mins)

Note: Grouping Options

  • Option 1: Crowd-source cracking - Continue as a whole class, with 2 students playing Bob and Alice, and everyone else playing Eve.

  • Option 2: Small group experimentation - Have previous Alice-and-Bob pairs get together in groups of 4. One pair plays Bob and Alice, the other pair plays Eve as a team of 2 (on one computer or two)

  • Students exchange numbers a few more times, trying to make it hard for Eve to crack. See how long it takes and what makes it hard. At what point would you feel "safe" as Alice or Bob that your messages were basically secure? As you play with the widget can you figure out why it works? Why can Alice decrypt the message but Eve can't?

(Optional) Part 5 - Use the "show all 3" version of the widget

  • Look at the "all" tab in the widget, which lets you act out and see all 3 characters at the same time by yourself. Try this out for a few rounds and see if you get a sense for why it works. Encourage students here to play with small values so the can get a sense of the relationships between the numbers.

Optional Recap Handout: There is an optional student handout that Recaps important ideas from the widget: (Optional) Public Key Cryptography Recap - Handout

Discussion (10 mins)

Discuss: What made the encryption harder/easier for Eve to crack?

  • Perhaps obvious, but the bigger the clock size the harder it is for Eve to crack.
  • There are also certain values that Bob could send, like 0 or 1, that would give away the secret.
  • There is no way to crack the encryption other than brute force
  • If you could imagine that value being not a 4-digit number but, say a 75-digit number the computation for Eve becomes mind bogglingly hard.

Discuss: Let's problem solve! The widget right now only lets you send one secret number at a time. Furthermore, it's kind of slow - it requires multiple trips over the internet to send one message. What's the fastest way you could use this tool (or any public key encryption) to send a secure text message?

Give students a moment to discuss and brainstorm.

  • Students will likely suggest using ASCII codes in some fashion - perhaps trying to cluster more than one ASCII character per message sent.
  • Note that if you're going to send multiple messages using public key cryptography you should change the public key occasionally, otherwise you're giving Eve more clues to crack the message with - you want Eve to start over every time.
  • A really clever thing to do is to only send one number that represents a key both parties can use for a good old fashioned symmetric encryption. In other words, only use (the slower, multi-trip) public key cryptography for the purpose of establishing a secret key to use in some other encryption method.
  • This is, in fact how HTTPS works - it uses public key cryptography to establish a secret key between two parties. Once established it uses a much faster encryption method for sending everything else.

Optional Discussion: According to the widget look at what Eve has to compute to crack Alice's private key. This reveals how Alice's public key was computed based on her choice of clock size and private key. Why are these made so that pvt * pub MOD clock = 1?

  • The only thing students really need to takeaway from this is that Alice's public key is no accident. It was computed to make the math in the end work out. That's all they need to know.
  • But, this fact - that the result of Alice's initial computation is 1 - is the crux of why the math works out in the end.
    • Short version: when Alice multiplies bob's encrypted message by her private key, it cancels out the public key portion of Bob's multiplication (because pvt * pub MOD clock = 1 it's just multiplying bob's number by 1), leaving only Bob's number remaining.
    • You can read a more thorough explanation here: How and Why Does the Public Key Crypto Really Work? - Resource

Remarks

This is as far as we're going to take the public key analogy. The public key crypto widget is a superficial version of RSA encryption. Instead of basic multiplication, RSA:

  • Uses numbers raised to powers of large prime numbers
  • Very large (256-bit) values for the modulo divisor (clock size)
  • Crack the encryption requires finding the prime factors of EXTREMELY large numbers. Prime factorization is much harder computational problem to solve than our little multiplication+mod problems here.

But from these activities hopefully you have a better sense of how public key encryption works and how making asymmetric keys is at least mathematically possible.

Wrap-up (10 mins)

Why this is important

Remarks

Public Key Encryption was (and is) considered a major breakthrough in computer science.

  • Public key cryptography is what makes secure transactions on the Internet possible.
  • In the history of the Internet, the creation of public key cryptography is one of the most significant innovations; without it we could not do much of what we take for granted today --we couldn’t buy things, communicate without being spied on, use banks, or keep our own conduct on the Internet secret or private.
  • Until asymmetric encryption was invented, the only way to ensure secure transactions on the Internet was to establish a shared private key, or to use a third party to guarantee security.
  • The implications of this are huge. It means any person can send any other person a secret message transmitting information over insecure channels!

Whittle it down

Goal: We want to ensure that we whittle down all of the various parts of this lesson and distill the things that are really important.

A lot of the activities, analogies and tools were in service of getting to some deep ideas about encryption and how it works. Ultimately, exposure to those deep ideas is helpful, but the actual facts that students need to know about Public Key Encryption are few.

Prompt: We just spent a lot of time learning about Public Key Cryptography through a bunch of different analogies, tools and activities. And what you've been exposed to mimics the real thing pretty closely. But what are the essential elements? Let's do a brain dump! List out what you think are the most important or crucial elements of Public Key Cryptography that you've learned.

Give students a few minutes to jot down their lists.

Pair & Share: Have students share their lists with an elbow partner. Then share to the whole group. Many valid points and ideas may emerge. Here are the key ones:

  1. Public Key Cryptography is a form of asymmetric encryption
  2. For Bob to send Alice a message, Bob must obtain Alice's public key
  3. The underlying mathematics ensure that both the public key and a message encrypted with the public key are computationally hard to crack while making it easy to decrypt with a private key
  4. It is strong because the method of encryption is publicly known, but keys are never exchanged.

There are some more detailed ideas about Public Key Cryptography that are interesting but not crucial for the AP Exam.

  • A public and private key are mathematically related so that decrypting is easy
  • The modulo operation acts as a one-way function to obscure inputs that are very large numbers
  • No one owns it - it's a public standard

Optional: Make a table applying terminology to the various analogies we saw

Fill in a table that shows all of the terms we've learned around public key encryption and how each analogy we've seen applies.

Lockbox Cups & Beans Public Key Crypto Widget
private key
public key
encrypted message
how to decrypt
how to crack

Assessment

Questions:

  1. In symmetric encryption, the same key is used to encrypt and decrypt a message. In asymmetric encryption different keys are used to encrypt and decrypt. Give at least one reason (more are welcome) why asymmetric encryption is useful.

  2. In the cups and beans activity, what is the public key? What is the private key? What is the unencrypted and encrypted message?

  3. What are some other examples of one-way functions? Can you think of a one-way function in real life?

  4. Using your name and the name of a friend, describe the process of sending your friend a message using public key cryptography. Your explanation should include the terms: Public Key, Private Key, Encrypt(ion), Decrypt(ion)

  5. Explain what the modulo operation does. You may use the analogy of a clock in your answer if you like.

  6. Why is modulo a one-way function?

  7. Describe to a person who knows nothing about encryption why public key encryption is hard to crack.

  8. What is 13 MOD 17?

    a) 0

    b) 1 4/13

    c) 4

    d) 13

    e) 17

  9. What is 20 MOD 15?

    a) 0

    b) 1.5

    c) 5

    d) 15

    e) 20

Extended Learning

View on Code Studio

Key Key: Mulitplication + Modulo

Big Picture:

This lesson has a lot of different parts to it. But all parts are necessary building blocks that lead to an answer to the crucial question:

How can two people send encrypted messages back and forth over insecure channels (the internet) without meeting ahead of time to agree on a secret key?

The answer explains what Public Key Cryptography is and how it works. In a nutshell, there are two main principles you need to understand, that we try to lead students through in this lesson:

Principle How we cover it in the lesson
1. The mechanics of communication with public key cryptography
  • Recall public/private key idea from the video
  • Teacher Demonstration: "Cups & Beans"
    		•
    2. The basic mathematical principles that make it possible
  • Thought Experiment: Modulo as a clock
  • The "Modulo Clock" Widget
  • Public Key Crypto Widget & Activity

    • Code studio is setup to walk students through these ideas with you (teacher) pausing at various points to lead a discussion, or run an activity.

    View on Code Studio

    Cups and Beans Activity

    You can either do this as a teacher demonstration (recommended) using: * Teacher Demonstration Guide: Public Key Bean Counting

    or, as student activity for groups of 3 using: * Student Activity Guide: Public Key Bean Counting (for groups of 3)

    Teacher Demonstration Synopsis:

    NOTE: more detailed instructions and teacher script can be found in the Teacher Demonstration Guide: Public Key Bean Counting

    • Introduce the characters "Alice, Bob and Eve"

    • Explain the "Cups & Beans" metaphor - how beans in a cup represents encrypted information

    • Demonstrate the Information Exchange process

      • Alice make a public key
      • Bob use public key to encrypt message
      • Alice decrypt
      • (Eve sees all information going back and forth but cannot decrypt)

    • Recap the mechanics of how public key cryptography works

    • Cups and Beans - What's the point?

    View on Code Studio

    Public Key Bean Counting (aka The "Cups & Beans" Activity)

    Sending Secret Messages without agreeing a on a secret key ahead of time

    In this activity, cups filled with beans will represent information going back and forth between Alice and Bob.

    The goal: understand the mechanics of communication using public and private keys

    The Metaphor: Beans inside the cup represent "encrypted information"

    Setup

    • Information will be represented as beans inside a cup
    • Alice will create a "public cup" of beans
    • Bob will add a secret number of beans
    • Eve can see everything, even pass the cup, but can't open it up -- can she determine the secret message?

    Teacher Demonstration (or activity)

    Once you have done the activity or seen the demonstration, consider this table of key terms and takeaways below.

    Main Takeaways and Terminology:

  • Obviously on the Internet information is not exchanged as beans in cups.
  • Our demonstration DOES NOT show or explain how the math or encryption works (we'll get to that next)
  • What it DOES show are the mechanics of public key communication: How public and private keys are used to encrypt information.
  • Here are the terms you should know:

    • View on Code Studio

    Modulo Clock Instructions

    • You can have students read these instructions or you can explain modulo and demonstrate how to use the widget yourself.

    • There is nothing special about the numbers we suggest using.

    • Make sure that students do experiment with small and large numbers for both the input value and clock size.
    View on Code Studio

    Clock Arithmetic (Modulo)

    The kind of "Clock Arithmetic" discussed (officially known as "modular arithmetic") is a one-way function because you can't tell what the input number was, just by looking at the clock face.

    Modulo

    The mathematical operation modulo is the remainder after dividing two whole numbers.

    We can visualize this idea as trying to count up to some number using a clock and seeing where the hand ends up.

    • For example: if you're trying to count up to 43 on a normal clock with 12 numbers.
    • You are doing: 43 MOD 12.
    • The result of 43 MOD 12 is: 7. Reason: 43 / 12 = 3 remainder 7

    The clock helps you see another way to think about division - how many times can I count up by 12s until I get to 43 without going over? 12...24...36. Then how much do I need to add to 36 to make it 43? Answer: 7 - that's the remainder.

    Do this: Experiment with the "Modulo Clock"

    • On the next page is a widget that let's you play with this idea
    • The widget helps you visualize the result of modular arithmetic
    • You can also make a clock of any size - you don't have to limit yourself to 12.
    • Experiment with different clock sizes and numbers.

    Using the Modulo Clock

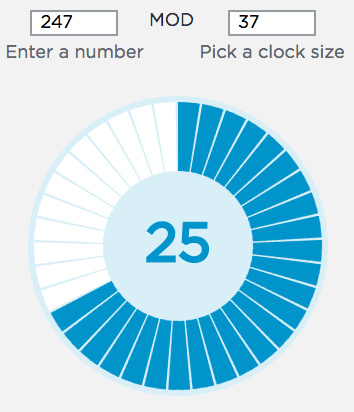
    You get to set two values - a number and the clock size. For example if you set number 45 with clock size 37 then

    Try the following for each:

    "Enter a number" "with clock size..."
    45 311
    300 311
    356 311

    Also try:

    • Numbers that are much smaller and much bigger than the clock size.
    • Try VERY large clock sizes too.
    View on Code Studio

    Public Key Crypto Widget Instructions

    You may want to put these student instructions up on the screen at the front of the room.

    You may also want to demonstrate with 3 students how it works to show that it is similar to the Cups and Beans activity.

    Common Misconceptions to look out for:

    Alice picks numbers essentially at random

    • Alice should pick a public modulus essentially at random - we provide a list to choose from. (That list happens to be all of the prime numbers less than 10,000)
    • Alice should pick her private key at random as well - this can be ANY number less than the public modulus.

    The widget is NOT networked in any way - the widget does not actually send messages to your partners. It is a standalone app that guides you through public key encryption process based on the character you chose.

    Where are these numbers coming from? * The widget does expose the math but every calculation is basically some version of ( x * y ) MOD z where:

    • (x * y) is always public number times a private number

    • z is the public modulus

    • Since the result of the multiplication is MODed, it makes it hard to figure out the private value, even if you know the public one. For example if the equation is:

      ( 65 * ___ ) MOD 257 = 30

    What should you plug into the blank space to make it work out? There is no way to figure it out besides trial and error. (It might take a little while to convince yourself this is true).

    View on Code Studio

    Public Key Crypto Widget Instructions

    In this activity you will simulate public key cryptography by:

    • Acting as Alice, Bob or Eve
    • Using a widget on your computer that will do computations for you
    • Speaking out loud to exchange information

    To do the activity...

    • Form a group of 3 people.
    • Choose your character: Alice, Bob, or Eve
    • Follow the instructions on the screen, each are individual to the character.
    • NOTE: Alice acts first - announcing two numbers publicly.

    • Notice that Bob's first instruction (shown at right), for example, is to wait until he hears Alice announce something.

    • This diagram shows the basic setup of computers and who says what.

    Background

    On the next page is the public key crypto widget. This widget will use numbers and math to do public key encryption, but it's important to understand that the mechanics of what you're doing are basically the same as the cups and beans activity

    The Goal just as before, is for Bob to send Alice a secret number. But for that to happen Alice actually has to act first to create a public key for Bob to use. So, using the widget the process is still:

    • Alice creates a private and public key
    • Bob uses the public key to encrypt a secret number
    • Eve can intercept all public information and tries to crack it.

    The differences between the public key crypto widget and the cups and beans activity:

    • All data are numbers - the secret messages are numbers that get encrypted by transforming them into other numbers. (This replaces secret numbers of beans "encrypted" by putting them in a cup).
    • Use your voice to broadcast encrypted information publicly (this replaces beans in a cup getting passed around)
    • The "public key" is actually a combination of two numbers - Alice will produce a "public key" number, but there is also a "public clock size" that is used to produce that number. Both are publicly known. Since the clock size could actually be declared by anyone, including Eve, we refer to Alice's public number as her "public key."
    • The Math: Multiplication and Modulo - rather than simple addition and subtraction of beans, we'll multiply numbers together as input to modulo.
    View on Code Studio

    Student Instructions

    In symmetric encryption the same key is used to encrypt and decrypt a message. In asymmetric encryption different keys are used to encrypt and decrypt. Give at least one reason why asymmetric encryption is useful

    View on Code Studio

    Teaching Tip

    Answers:

    • The number of beans Alice chooses to put in the cup initially: Private key
    • A sealed cup of beans that Alice puts on the table: Public key
    • Bob adding beans to the cup: Encrypting a message
    • Alice dumping the beans out of the cup and counting off her original number: Decrypting a message

    Student Instructions

    View on Code Studio

    Student Instructions

    Explain in your own words what the modulo operation does. You may use the analogy of a clock in your answer if you like.

    View on Code Studio

    Teaching Tip

    Answer:

    • 5

    Student Instructions

    View on Code Studio

    Teaching Tip

    Answer:

    • 13

    Student Instructions

    View on Code Studio

    Student Instructions

    Describe to a person who knows nothing about encryption why public key encryption is secure and is hard to crack.

    Standards Alignment

    View full course alignment

    CSTA K-12 Computer Science Standards (2011)

    CPP - Computing Practice & Programming
    • CPP.L3A:9 - Explain the principles of security by examining encryption, cryptography, and authentication techniques.
    • CPP.L3B:5 - Deploy principles of security by implementing encryption and authentication strategies.
    CT - Computational Thinking
    • CT.L3B:2 - Explain the value of heuristic algorithms to approximate solutions for intractable problems.
    • CT.L3B:3 - Critically examine classical algorithms and implement an original algorithm.
    • CT.L3B:4 - Evaluate algorithms by their efficiency, correctness, and clarity.
    • CT.L3B:5 - Use data analysis to enhance understanding of complex natural and human systems.

    Computer Science Principles

    4.2 - Algorithms can solve many but not all computational problems.
    4.2.1 - Explain the difference between algorithms that run in a reasonable time and those that do not run in a reasonable time. [P1]
    • 4.2.1A - Many problems can be solved in a reasonable time.
    • 4.2.1B - Reasonable time means that as the input size grows, the number of steps the algorithm takes is proportional to the square (or cube, fourth power, fifth power, etc.) of the size of the input.
    • 4.2.1C - Some problems cannot be solved in a reasonable time, even for small input sizes.
    • 4.2.1D - Some problems can be solved but not in a reasonable time. In these cases, heuristic approaches may be helpful to find solutions in reasonable time.
    4.2.2 - Explain the difference between solvable and unsolvable problems in computer science. [P1]
    • 4.2.2A - A heuristic is a technique that may allow us to find an approximate solution when typical methods fail to find an exact solution.
    4.2.3 - Explain the existence of undecidable problems in computer science. [P1]
    • 4.2.3A - An undecidable problem may have instances that have an algorithmic solution, but there is no algorithmic solution that solves all instances of the problem.
    4.2.4 - Evaluate algorithms analytically and empirically for efficiency, correctness, and clarity. [P4]
    • 4.2.4A - Determining an algorithm’s efficiency is done by reasoning formally or mathematically about the algorithm.
    • 4.2.4B - Empirical analysis of an algorithm is done by implementing the algorithm and running it on different inputs.
    • 4.2.4C - The correctness of an algorithm is determined by reasoning formally or mathematically about the algorithm, not by testing an implementation of the algorithm.
    6.3 - Cybersecurity is an important concern for the Internet and the systems built on it.
    6.3.1 - Identify existing cybersecurity concerns and potential options to address these issues with the Internet and the systems built on it. [P1]
    • 6.3.1H - Cryptography is essential to many models of cybersecurity.
    • 6.3.1I - Cryptography has a mathematical foundation.
    • 6.3.1L - Public key encryption, which is not symmetric, is an encryption method that is widely used because of the enhanced security associated with its use.

    CSTA K-12 Computer Science Standards (2017)

    NI - Networks & the Internet
    • 2-NI-06 - Apply multiple methods of encryption to model the secure transmission of information.
    • 3A-NI-07 - Compare various security measures, considering tradeoffs between the usability and security of a computer system.
    • 3B-NI-04 - Compare ways software developers protect devices and information from unauthorized access.